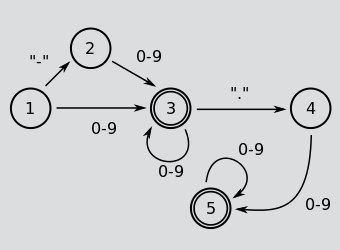
The machine starts at (1), possibly matches minus sign, then processes as many digits as required.
After that, it may match a dot (3->4) which must be followed by one digit (4->5), but maybe more.
The classic example of a non-regular language is a family of strings like:
a-b
aaa-bbb
aaaaa-bbbbb
Formally, we need a line that consists of N occurrences of a, then -, then N occurrences of b.
N is any integer greater than zero.
You can't do it with a finite machine, because you have to remember the number of a chars you encountered which leads you to the infinite number of states.
Regular expressions can match only regular languages.
Remember to check whether the line you are trying to process can be handled by FSM at all.
JSON, XML or even simple arithmetic expression with nested brackets cannot be.
Mind, however, that a lot of modern regular expression engines are not regular.
For example, Python regex module supports recursion
(which will help with that aaa-bbb problem).